Supply Chain Optimization — It’s Not Magic, It’s Mathematics
Companies with complex supply chains must make real-time, data-driven decisions to ensure efficient resource utilization and first-class customer service. Yet, many organizations continue to rely on outdated planning tools such as spreadsheets and MRP. Supply chain planning based on mathematical optimization is fundamentally different from traditional methods and allows companies to maximize overall supply chain performance. This article uses common planning scenarios to explain how supply chain optimization technology works and why companies looking to streamline operations and maximize profits should consider switching.
Optimization — Not just for Big Business
Supply chain optimization software has been around for decades, but it’s only recently that the technology has become a viable alternative for small and mid-size businesses. Today, the processing power required to run the optimization algorithms comes at a fraction of the cost. At the same time, supply chain optimization software has become more user-friendly and easier to maintain. Thanks to these advances, smaller organizations with limited IT budgets and resources can now benefit from this powerful technology.
Why do I need optimization?
Optimization software transforms the way companies plan and manage their supply chains. Because the optimization engine takes supply chain constraints and costs into account, the system-generated plans are validated upfront. The software can therefore provide the planner with more accurate decision support. The result is better customer service and resource utilization with less inventory - all helping to boost the bottom line. These instant benefits are why optimization implementations offer such an attractive ROI.
How does supply chain optimization work?
As humans, we trust the familiar and what we understand. Therefore, it’s essential for companies that rely on spreadsheets and MRP software to take the time to understand the fundamental differences between traditional planning tools and modern solutions powered by mathematical optimization. While there’s no need for planners and business users to understand the inner workings of mathematical modeling and optimization techniques, a good grasp of what underpins the planning approach is needed. To help with this understanding, let’s take a closer look at the three core elements of a supply chain optimization solution:
The Supply Chain Model (the “Digital “Twin”)
The Digital Twin is an electronic representation of your physical supply chain. It’s a detailed model of your processes and resources, with their associated costs and constraints. The model provides the blueprint for your planning solution. Warehouses, production lines, machines, vehicles, tooling, and staff are all represented here.
System Interfaces
The planning tool needs accurate, up-to-date information from your existing business systems. Depending on your setup, direct interfaces with ERP, PLM, CRM, and Transportation & Warehouse Management systems provide access to the necessary input data. Examples of required information are sales forecasts, customer orders, product information, and stock levels.
The Solver
The solver is the brain of the optimization solution and where the magic happens. It contains mathematical algorithms that work together to solve the supply chain problem described by the digital twin and the input data.
The solver optimizes one of the two available “objective functions”:
A. Maximum Profit
B. Max Delivery Service at Lowest Cost
If revenue is represented in the model, the solver will determine the plan that maximizes your overall profitability. However, if revenue is not included in the model, the solver will maximize customer service at the lowest possible cost. It is important to be aware of the difference between these two objective functions. However, in both cases, the solver will find the best overall solution for the business with respect to the defined business rules and constraints.
Optimization Examples
To get a better feel for the difference between optimization technology and traditional planning approaches, we can look at some common planning problems.
EXAMPLE 1 — STOCK BUILD
Let’s start with a stock build, essential for businesses dealing with seasonality or big promotions that cause peaks in demand. We have two basic options; to gradually build up the required stock over time or to add extra capacity closer to the peak. Gradually building up stock allows us to maintain a steady, cost-efficient production and to make use of any spare capacity. But it also requires us to hold stock for longer with higher storage and handling costs and an increased risk of expiry and obsolescence. The diagrams below show how we gradually build stock by maintaining a steady utilization of the line (40 hours per week) ahead of the peak in demand during week 29 – 32.
Stock Build Over Longer Time Period
The other alternative is adding more production capacity closer to the peak in demand by adding extra in-house capacity or outsourcing. This approach keeps inventory levels and inventory-related costs low, but the additional production capacity usually comes at a premium, if at all available.
Stock Build Using Extra Capacity Closer to Peak in Demand
The above graphics show the difference between the two, both potentially viable, alternatives. But which one is our best option? It could even be a combination of the two. If we only look at one product in isolation, this is not a difficult problem. But in a more realistic scenario, with hundreds or even thousands of products competing for production and distribution capacity across multiple sites, the optimal solution is often anything but obvious, sometimes even surprising.
Planning The Stock-Build With Optimization
Planning always involves tradeoffs. A supply chain optimization solution automatically determines the stock-build strategy that best satisfies your overall business goals – be it to maximize overall profits or meet customer service targets at the lowest possible cost. Crucially, when determining the stock-build strategy, the mathematical solver takes the entire supply chain into account. If the focus is solely on the stock-build product, the business as a whole is likely to suffer. To perform the mathematical optimization, the solver needs access to the data that frames the planning problem. In our example, the supply chain model defines the costs and constraints relating to overtime, cost of capital, product expiry, batch sizing, product mix, and more. And with direct access to demand and on-hand stock information from 3rd party systems, the solver has everything it needs to calculate the optimal plan.
Planning The Stock-Build Without Optimization
Planning the same stock build using the MRP and DRP functionality of an ERP system is an entirely different challenge. With tools that don’t consider production and inventory constraints, the planner is left with a lot of work to validate the plan’s basic feasibility. Unable to recognize planning constraints, MRP and DRP must make a series of assumptions, including infinite capacity and fixed production and distribution lead times. However, capacity is rarely unlimited, and lead times are, per definition, not fixed. Instead, they depend on the availability of materials and production, storage, and distribution capacity. As a result, MRP-generated plans are of much lower quality. MRP’s inability to deliver a plan that can be executed “out-of-the-box” is only part of the problem. Because MRP doesn’t consider the plan’s overall profitability, it is difficult to determine if it meets the company’s business goals.
EXAMPLE 2 — PRoduct Mix
In our second example, we take a closer look at how the system uses mathematical modeling to optimize a planning problem. The planning scenario is a bakery that wants to determine an optimal product mix. To make things simple, we only consider two products, bread and brownies, and two ingredients – flour and sugar.
Optimizing The Product Mix With Optimization
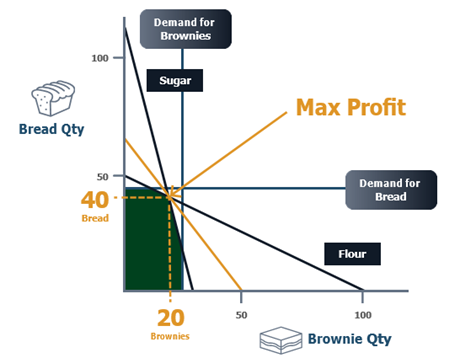
1. The flour supply is limited to 50kg for the period. The planning system accesses the product BoMs and sees that a bread requires 1kg of flour and a brownie ½ kg. The graph below shows the flour constraint.
2. After adding the supply constraint for sugar, we get the following picture. Our possible product mix is now reduced.
3. Next, the demand forecasts for the two products, bread (45) & brownies (25), are imported from the demand planner. As we don’t want to produce more than what we have demand for, the possible product mix is further reduced.
4. The optimal product mix is where the bakery achieves maximum profit. With a profit contribution of $1.50 for bread and $2.00 for brownies, the system has all the information it needs to determine the optimal mix.
5. In this example, a Linear Programming (LP) algorithm is used to determine the optimal product mix. The system establishes the profit contribution line and finds the optimum. Remember - all this happens automatically!
“There are several different algorithms available depending on the mathematical structure of the planning problem. In this example, the system chooses an optimization technique called Linear Programming. Crucially, the planner doesn’t need to be a mathematician to use the system, as this is all taken care of automatically.”
6. The optimal product mix is 40 breads and 20 brownies.
The above example is very simple, but the beauty of mathematical optimization is that we can achieve the same optimized results with thousands of products, limited supply materials, and capacity-constrained production, storage, and transportation resources.
Optimizing The Product Mix Without Optimization
Without optimization, the pattern from our first example will repeat itself. An MRP-generated plan will produce the total demand quantity of 45 breads and 25 brownies, despite the limited supply of flour. While the system will recognize the resulting shortage of flour, this will only be clear to the planner after the fact. Thus, it is down to the planner to resolve the problem.
Changing The Role Of The Planner
Working with an MRP system (without mathematical optimization) is very different from a supply chain optimization solution. With MRP, planners are notified when there’s an issue but left to figure out how to fix the problem themselves. This is time-consuming and invariably leads to sub-optimal decisions based on gut feel and bias rather than real-time data and facts. With supply chain optimization, planning becomes much more proactive and strategic to the organization. With a system that models and optimizes the entire supply chain, planners and managers have complete visibility of all activities and how they interrelate. When someone makes a change to the plan, any ripple effects are immediately visible.
How Optimization Impacts The Role Of The Planner
Improved planning automation means more time to focus on exceptions.
The plans can be executed “out-of-the-box” with little or no need for manual adjustment.
The planning function will become more strategic when trust continues to grow.
The speed of the optimization algorithms allows planners to run multiple what-if analyses before making important decisions.
The planner will maintain the “digital twin”, keeping business rules, costs, and constraints up to date.
In Summary
Supply chain planning based on mathematical optimization has the power to transform your business. The technology is mature and proven to add significant value and it is now available and affordable to companies of all sizes. Any manufacturing or distribution organization not yet using supply chain optimization is strongly encouraged to find out what it would mean to their customer service and bottom line.
Establish is a supply chain consulting firm focusing on supply chain strategy, transportation consulting services, warehouse design & improvements and supply chain planning.